Solution Steps P ( x ) = ( x 4 ) ( x 2 ) ( x 1 ) P ( x) = ( x 4) ( x 2) ( x − 1) Apply the distributive property by multiplying each term of x4 by each term of x2 Apply the distributive property by multiplying each term of x 4 by each term of x 2Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us! Click here 👆 to get an answer to your question ️ Find p(x 1) if p(x) = x^2 – 3x – 1 everkayy everkayy Mathematics High School answered Find p(x 1) if p(x) = x^2 – 3x – 1 1 See answer everkayy is waiting for your help Add your answer and earn points

If X 1 2 Is The Zero Of The Polynomial P X 8x3 Ax2 X 2 Find The Value Of A Maths Meritnation Com
P(x)=x^3-2x^2-8x-1 g(x)=x+1
P(x)=x^3-2x^2-8x-1 g(x)=x+1- The underlying distribution makes no difference Therefore, the answer is 1 / 6 Had these not been IID then you'd need to do more work and the answer would depend on how they are distributed, but in this case, the variables are exchangeable Share answered Oct 30 ' atP(X =0) = 1 16,P(X =1) = 4 16,P(X =2) = 6 16,P(X =3) = 4 16,P(X =4) = 1 16 (1) Notice that the denominators of the five fractions are the same and the numerators of the five fractions are 1, 4, 6, 4, 1 The numbers in the numeratorsis a setof binomial coefficients 1 16 = 4 0 1 16, 4 16 = 4 1 1 16, 6 16 = 4 2 1 16, 4 16 = 4 3 1 16, 1 16 = 4




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf
1x2at Sportwetten und Casino Brasilien Campeonato Brasileiro Serie , Frauen, Playoffs 1,50The points (x,y,z) of the sphere x 2 y 2 z 2 = 1, satisfying the condition x = 05, are a circle y 2 z 2 = 075 of radius on the plane x = 05 The inequality y ≤ 075 holds on an arc The length of the arc is 5/6 of the length of the circle, which is why the conditional probability is equal to 5/6P(q(x)) p ( q ( x)) Evaluate p(q(x)) p ( q ( x)) by substituting in the value of q q into p p p(2x−1) = −2(2x−1) 1 p ( 2 x 1) = 2 ( 2 x 1) 1 Simplify each term Tap for more steps Apply the distributive property p ( 2 x − 1) = − 2 ( 2 x) − 2 ⋅ − 1 1 p ( 2 x 1) = 2 ( 2 x) 2 ⋅ 1 1 Multiply 2 2 by −
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyThe probability of having x successes in n trials is (where x!Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history
X n x n − px (1p) nx VAR(X) = np(1p) = 3* 03 * 07 = 063 SD(X) = np(1p) Calculations shown for Binomial (n=3, p=03) = 0794 Note this is equivalent to counting success = 1 and failure = 0Click here👆to get an answer to your question ️ If p(x) = x^2 2 √(2)x 1 , then p(2√(2)) is equal to Join / Login > 10th > Maths > Polynomials > Relationship between ZeroesNew questions in Mathematics




If It Was X 2 2x 1 X 2 Then How Would You Do It I Let P X 2x2 X Maths Polynomials Meritnation Com




Polynomial 1 Class 9 Notes
p (x)=x²2√2x1 p (2√2)= (2√2)² (2√2*2√2)1 p (2√2)= (2√2)² (2√2)²1 =01 =1 Therefore, the answer is 1 Thank you Hope this will help you mitgliedd1 and 1355 more users found this answer helpfulFinally, using distributive property and foil, you would get x^2xx^23x2=(x^2x2)2x^22x2=x^2x23x^23x=0 3x(x1)x=0 and x=1 ( thats only if the big X is the same as the small xs) You are right, thank you SO MUCH!!Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




Polynomials Ppt Video Online Download



Find The Values Of P And Q For Which F X 1 Sin 3 X 3cos 2 X If X Pi 2 And P If X Pi 2 Sarthaks Econnect Largest Online Education Community
BASIC STATISTICS 5 VarX= σ2 X = EX 2 − (EX)2 = EX2 − µ2 X (22) ⇒ EX2 = σ2 X − µ 2 X 24 Unbiased Statistics We say that a statistic T(X)is an unbiased statistic for the parameter θ of theunderlying probabilitydistributionifET(X)=θGiventhisdefinition,X¯ isanunbiasedstatistic for µ,and S2 is an unbiased statisticfor σ2 in a random sample 3Westbrass R x 11/2 in PTrap with High Box Flange, Matte Black Reviews, So you can check out the other reviews at AmazoncomThe answer should be 22 As P (Q (x)) = P (x)R (x) P (x) = (x1) (x2) (x3) (Q (x) 1) (Q (x) 2) (Q (x) 3) = (x1) (x2) (x3)R (x) And R (x) is a 3 degree polynomial So, Q (x) should be a 2 degree polynomial We can write R (x) as (xa) (xb) (xb) because it is a 3 degree polynomial
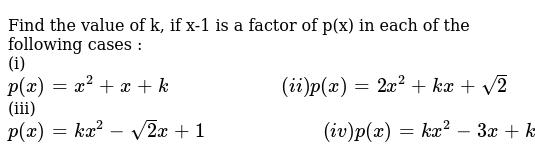



Find The Value Of K If X 1 Is A Factor Of P X In Each Of The Fol




If P X 2x 2 3x 5 Then Find The Value Of P 0 P 1 Whole Devided By P 1 Maths Polynomials Meritnation Com
77k views asked in Class IX Maths by ashu Premium (930 points) If p (x) = x2 – 2√2x 1, then p (2√2) is equal to (a) 0 (b) 1 (c) 4√2 (d) 8 √2 1 polynomials The Attempt at a Solution P (X 1 < X 2 < X 3) = triple integral of e (x1x2x3) dx 2 dx 1 dx 3 as x 2 goes from x 1 to x 3, x 1 goes from 0 to x 2 and x 3 goes from x 2 to infinity When I solve this integral I get 0 for an answer The back of the book suggests the answer is 1/6 Explanation (x −1)(x 2) aaaaaaaaaaaaax − 1 aaaaaaaaaaa × x 2 −−−− − aaaaaaaaaaaaax2 − x aaaaaaaaaaaaaaaa2x − 2 aaaaaaaaaaaaaa¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯x2 x − 2




P 1 Actuary Exam Question Mathematics Stack Exchange



Madasmaths Com Archive Maths Booklets Basic Topics Various Polynomials Exam Questions Intro Pdf
Show 1 and 1 are only solutions to x^2 = 1 (mod p^2) for odd prime p Let p be an odd prime and n be an integer Show that 1 and 1 and the only solutions to x 2 ≡ 1 m o d p n Hint What does a ≡ b m o d m mean, then think a bit for k an integer1x2at Sportwetten und Casino Today`s offer Complete offer Back Sport SportThis preview shows page 123 126 out of 360 pages X 0 P (X 0) A 0 1 B 0 2 C 0 3 D 0 4 (a) 2 pts Fill in the table below with the distribution of Waldo's location at time t = 1 X t P (X 1) A 0 1 * 0 8 0 2 * 0 3 = 0 14 B 0 2 * 0 5 0 1 * 0 2 0 3 * 0 3 = 0 21 C 0 3 * 0 5 0 4 * 0 3 0 2 * 0 2 = 0 31 D 0 4 * 0 7 0 3 * 0 2 = 0 34 (b) 3 pts F T (X) is




Factoring Polynomials Ppt Download




If X 1 2 Is The Zero Of The Polynomial P X 8x3 Ax2 X 2 Find The Value Of A Maths Meritnation Com
1/2 in x 5 in Black Steel Nipple STZ nipples are the way to go when selecting STZ nipples are the way to go when selecting gas pipe for your residence Our durable, schedule 40 black steel is hydrostatically tested 8 Comments 5 Solutions 2,391 Views Last Modified The solution to a problem is P (x) = (x1) (x2) (xn) (for some integer n) However, I want to expand this polynomial, so as to find the coefficient of the ith power It's quite clear that a_n=1, and a_0=n!Then, f(x)g(x) = 4x 2 4x 1 = 1 Thus deg( f ⋅ g ) = 0 which is not greater than the degrees of f and g (which each had degree 1) Since the norm function is not defined for the zero element of the ring, we consider the degree of the polynomial f ( x ) = 0 to also be undefined so that it follows the rules of a norm in a Euclidean domain




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Toppers Bulletin




Ex 2 2 3 Verify Whether Following Are Zeroes Of The Ex 2 2
(1−x)2 X∞ k=0 (k1)2xk = S 2 = 1x (1−x)3 2 Geometric Distributions Suppose that we conduct a sequence of Bernoulli (p)trials, that is each trial has a success probability of 0 < p < 1 and a failure probability of 1−p The geometric distribution is given byDivide f2, the coefficient of the x term, by 2 to get \frac{f}{2}1 Then add the square of \frac{f}{2}1 to both sides of the equation This step makes the left hand side of the equation a perfect square so to attain P (x) = 0, we go for random negative numbers, let us try x = 1 we get P (1) = 2, let us try x = 1/2, here P (1/2) = 0 is found, so this is our first value this way our first x = 1/2 is easily spotted then we need to find other 3 remaining values, we divide the given polynomial by (x05), the equation we get is 2x^3 14 x^2 24x 8,




Ex 2 2 3 Verify Whether Following Are Zeroes Of The Ex 2 2
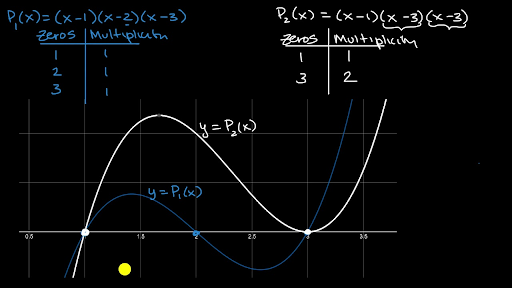



Multiplicity Of Zeros Of Polynomials Video Khan Academy
Number of successes in n trials We can write X as follows X=X 1 X 2 KX n where !Click here👆to get an answer to your question ️ If alpha, beta are roots of x^2 p ( x 1 ) c = 0 Show thati) ( alpha 1 ) ( beta 1 ) = 1 c &ii) alpha^22alpha1alpha^22alphac beta^22beta1beta^22betac = 1Advanced Math questions and answers Let P (x) = x4 x 1 Let kı = 5 mod 2 and k2 = 6 mod 2 Let A (x) = x3 k1x2 1 and B (x) = x2 k1x 1 Compute Clx) mod P (x) in GF (24) for (a) (b) (d) C (x) = A (x) B (x), C (x) = A (x)B (x), C (x) = () C (x) = B2 (x) Question Let P (x) = x4 x 1 Let kı = 5 mod 2 and k2 = 6 mod 2




Ch 1 2




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 2 Cbsetuts Com
X (x1) (x2) (x3)=1 Simple and best practice solution for x (x1) (x2) (x3)=1 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and letP*(x)(x*(x^21))=0 Step by step solution Step 1 Trying to factor as a Difference of Squares 11 Factoring x 21 Theory A difference of two perfect squares, A 2 B 2 can be factored into (AB) • (AB) Proof (AB) • (AB) = A 2 AB BA B 2 = A 2 AB AB B 2 = A 2 B 2 Note AB = BA is the commutative property of multiplication Explanation According to Viete's Theorem if P (x) has a factor of (x −a) then a is a root of this polynomial, so in this case this polynomial has 2 roots x3 = − 1 and x4 = 2 To find the other roots you have to divide P (x) by (x − 2)(x 1) The result will be x2 5x 6 Then you can calculate the remaining roots



Check Whether P X Is A Multiple Of G X Or Not Studyrankersonline




Polynomials Ppt Video Online Download
Now, when we see the 2nd half of the question, where you have written "Find the Remainder when P(x) is divided by (x1)(x2)" I think that this is an incorrect statement as if you see carefully you might notice that here divident or P(x) ie 3x 8 (which we calculated above) is smaller than (x1)(x2) and such a division will not give a12 p2 2px x2 is a perfect square It factors into (px)• (px) which is another way of writing (px)2 How to recognize a perfect square trinomial • It has three terms • Two of its terms are perfect squares themselves • The remaining term is twice the product of the square roots of the other two termsGraph P(x)=(x1)(x1)(x2) Find the point at Tap for more steps Replace the variable with in the expression Simplify the result Tap for more steps Simplify each term Tap for more steps Raising to any positive power yields Raising to any positive power yields Multiply by Multiply by




The Polynomials P X 2x Cube Kx Square 3x 5 And Q X X Cube 2x Square X K When Divided By X 2 Leave The Remainders R1 And R2 Respectively Find




Verify Whether The Following Are Zeroes Of The Polynomial Indica
CobbDouglas utility function MRS = a 1 − a x 2 x 1 = p 1 p 2 p 1 x 1 p 2 x 2 = m bracerightBigg → (x ∗ 1, x ∗ 2) = parenleftbigg am p 1, (1 − a) m p 2 parenrightbigg II Nontangent solution A Kinked demand Example Perfect complement u (x 1, x 2) = min {x 1, x 2} 18 Downloaded by Themegaamind edits (email protected) lOMoARcPSD(1)^n, but I've yet to figure a pattern for the others" # = 0 if trial i is a failure 1ftrialiisasuce X i The X i's are Bernoulli random variables with parameter p E(X i)=1*p0*(1!p)=p E(X)=E(X 1)E(X 2)KE(X n)=np Ex A group of N people throw their hats into the center of a room The hats are mixed, and



On Dividing 3x3 2x2 5x 5 By A Polynomial P X The Quotient And The Remainder Are X2 X 2 And 7 Respectively Find P X Mathematics Topperlearning Com Ysf8guuhh
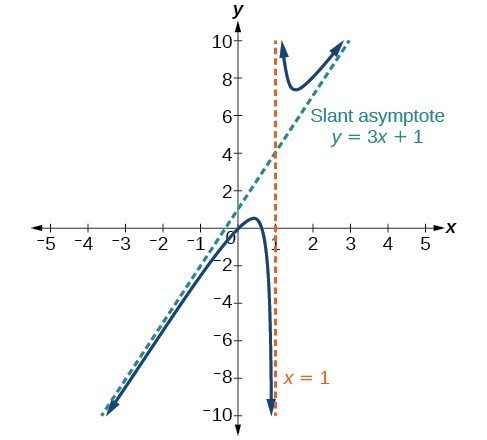



Identify Horizontal Asymptotes College Algebra
= x(x1)(x2)1, and 0!Expanding brackets Binomials The distributive property of multiplication over addition The distributive property of multiplication over subtractionDistriSimple and best practice solution for p(x)=x^21 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,



If P X X2 4x 3 Then Evaluate P 2 P 1 P 1 2 Studyrankersonline




If X 1 2 Is A Zero Of The Polynomial P X 8x 3 A X 2 X 2
= 1) E(X) = np = 3* 03 = 09 P(X=x)=!( )!!X = x 1, x = x 2, , x = x k, where x 1, x 2, , x k are roots of Q(x) To find the vertical asymptotes of f(x) be sure that it is in lowest terms by canceling any common factors, and then find the roots of Q(x) 3 Oblique Asymptotes The rational function f(x) = P(x If x^2 x 1 is a factor of the polynomial 3x^2 8x^2 8x 3 5k, then the value of k is A 0 B 2/5 asked Apr 21 in Polynomials by Cammy ( 273k points) factorization of polynomials




3 Verify Whether The Following Are Zeroes Of The Polynomial Indicated Against Them N 1 Quad P X 3 X 1 X Frac 1 3 N Ii P X 5 X Pi X Frac 4 5 N Iii P X X 2 1 X 1 1 N Iv P X X 1 X 2 X 1 2 N




Module 1 Polynomial Functions
If α is the positive root of the equation, p(x) = x 2 – x – 2 = 0, then lim x→α (√1cos(p(x)))/(x α 4) is equal to (1) 3/√2 (2) 3/2 (3) 1/√2 (4) 1/2 For example, $(1x)^2 = 1 2x 1 x^2$, and so the coefficients $1, 2, 1$ translate into the column vector $ \begin{bmatrix} 1 \\ 2 \\ 1 \end{bmatrix}$ Because $\dim \mathbf{P}_2 = 3$, this set is a basis if and only if these three vectors are linearly independent



1




Ex 2 2 3 Verify Whether Following Are Zeroes Of The Ex 2 2



If Both X 2 And X 1 2 Are Factors Of Px2 5x R Then Show That P R Studyrankersonline



Cbse 9 Math Cbse Polynomials Ncert Solutions



Check Whether 7 3x Is A Factor Of 3x3 7x




Ex 2 4 3 Find Value Of K If X 1 Is A Factor Of P X




Divide The Polynomial P X By The Polynomial G X And Find The Quotient And Remainder In Each Of The Following P X X 4 3x 2 4x 5 G X X 2




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Toppers Bulletin




If P X X 1 X 1 Then The Value Of P 0 P 1 And P 2 Are Brainly In




Example 4 Find A Zero Of The Polynomial P X 2x 1 Examples




If P X X X X 1 Then Find The Value Of P 1 P 1 2 Brainly In




Rd Sharma Solutions For Class 10 Chapter 8 Quadratic Equations Exercise 8 6 Avail Pdf




By Remainder Theorem Find The Remainder When P X Is Divided By G X I P X X 3 2x 2 Youtube



Cbse 9 Math Cbse Polynomials Ncert Solutions



Www Math Kth Se Math Gru 12 13 Sf1610 Cinte Mastertheorem Pdf



Cbse 10 Math Cbse Polynomials Ncert Solutions




Ex 2 2 2 Find P 0 P 1 And P 2 For Each Of The Ex 2 2




Ex 2 2 3 Verify Whether Following Are Zeroes Of The Ex 2 2




Polynomial 1 Class 9 Notes




Verify Whether The Following Are Zeroes Of The Polynomial Indica



2




Iii X 2 Find P 0 P 1 And P 2 For Each Of The Following Scholr




Verify Whether The Following Are Zeroes Of The Polynomial Indica



What Will Be The Value Of P And Q For X 2 2x 5 To Be A Factor Of X 4 Px 2 Q Quora
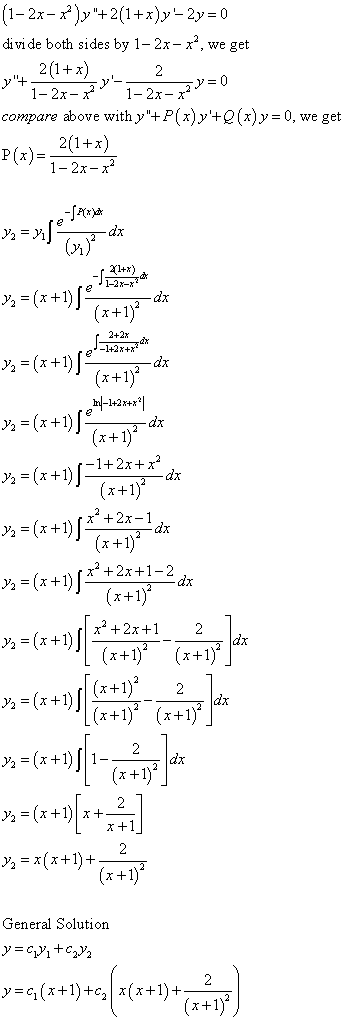



Differential Equations Solved Examples Reduction Of Order Formula Second Solution 1 2x X 2 Y 2 1 X Y 2y 0 Y1 X X 1




Module 1 Polynomial Functions



Let P X Be A Cubic Polynomial Whose Leading Coefficient Is 1 P 1 1 P 2 2 P 3 3 What Is Value Of P 4 Quora




If X2 X 1 Is A Factor Of X4 Px3 Qx2 1 Then Can The Values Of P And Q Be 1 2 1 2 1 2 3 1 2 4 2 1 Quora




If P X X2 4x 3 Evaluate P 2 P 1 P 1 2 Maths Polynomials I Meritnation Com




Polynomial 1 Class 9 Notes




Why 1 4 And 1 Zeroes Of The Polynomial P X 4x 2 3x 1 Brainly In




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf




If The Sum Of Zeroes Of P X A 1 X 2 2a 3 X 3a 4 Is 1 Find Its Product




The Random Variable X Has A Poisson Distribution If P X 1 0 P X 2 0 Then Find P X 3 Mathematics 3 Question Answer Collection



P X X 5




Horner S Method Wikipedia




If X 12 Is A Zero Of The Polynomial P X 8x 3 Ax 2 X 3 Find The Value Of A




Unit I Random Variables Part A Two Marks Pdf Free Download



Chapter 3 Interpolation George Mason University Flip Ebook Pages 1 46 Anyflip Anyflip



If X 1 2 Is A Zero Of The Polynomial P X 8x 3 Ax 2 X 2 Find The Value Of A Sarthaks Econnect Largest Online Education Community




Lim X 1 X 4 3 X 3 2 X 3 5 X 2 3 X 1 Mathematics Shaalaa Com




If X 2 And X 1 2 Are Factors Of Px2 5x R Then Show That P R Mathematics Topperlearning Com H4otppoo




Ex 2 2 3 Verify Whether Following Are Zeroes Of The Ex 2 2




Resolve 2x 3 X 1 X 2 1 2 Into Partial Fractions Youtube




The Linear Transformation L Defined By L P X Chegg Com




Ex 2 2 3 Verify Whether Following Are Zeroes Of The Ex 2 2



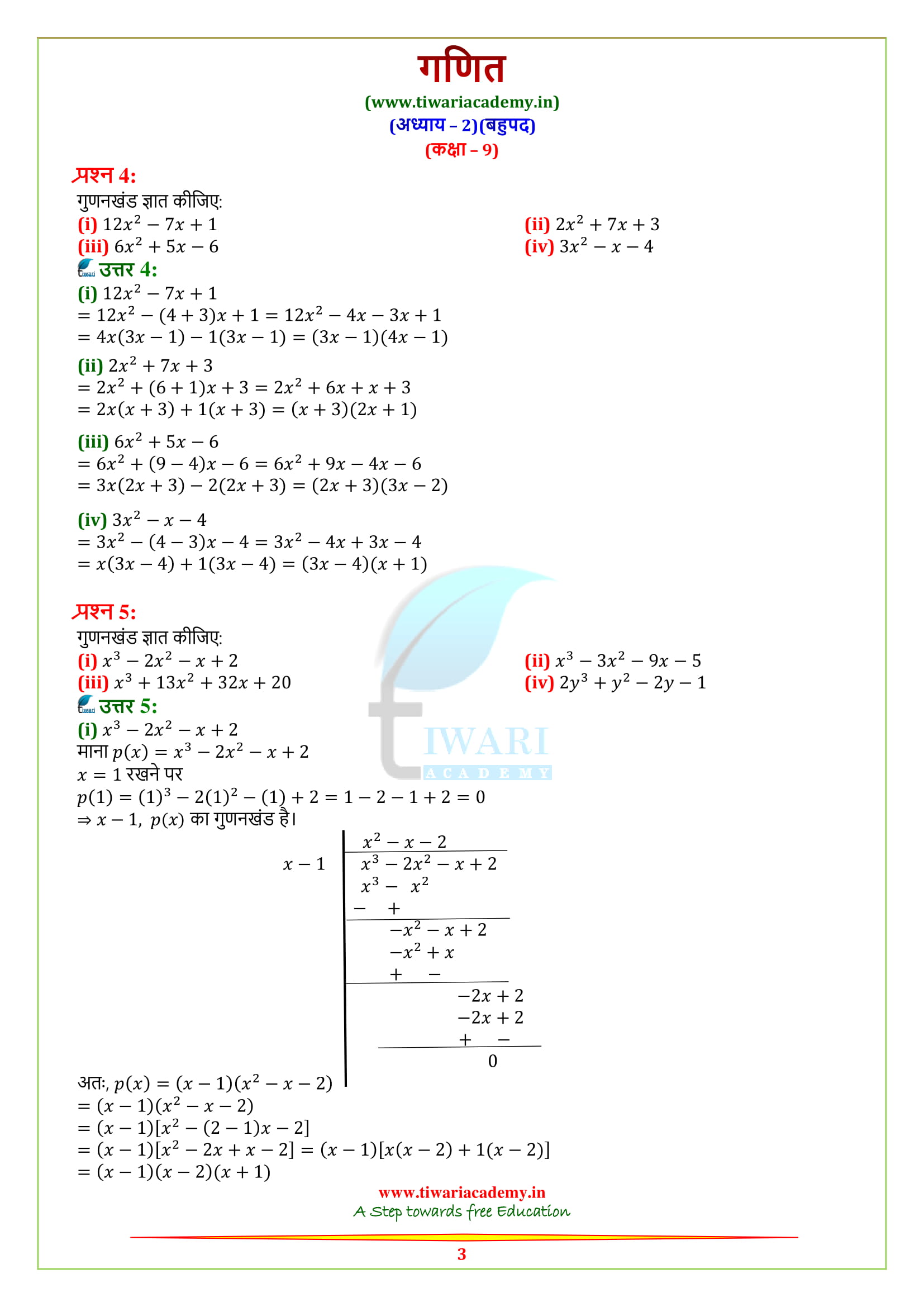
How To Factoize Factorise X3 2 2 X 2 Ii X3 3 2 9x 5 Iii X3 13 2 32x Iv 2y3 Y2 2y 1 Pushpender86 S Blog




Zeros Of P X




If P X X 1 X 1 Then The Value Of P 2 P 1 P 0 Isa 2b 4c 1 Brainly In




The Cumulative Distribution Function For A Certain Chegg Com




Find P 0 P 1 P 2 For The Polynomial P X X 1 X 2 Brainly In




Important Short Objective Questions And Answers Two Dimensional Random Variables




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Verify Whether The Following Are Zeros Of The Polynomial Indicated Against Them Or Not I Brainly In




Find P 0 P 1 And P 2 For Each Of The Following Polynomials I P Y Y 2 Y 1 Ii P T 2 T 2t 2 T 3 Iii P X X 3 Iv P X X 1 X 1




Remainder Theorem Examples Video Khan Academy




Ml Aggarwal Solutions For Class 10 Chapter 5 Quadratic Equations In One Variable Free Pdf Available




Verify Whether The Following Are Zeroes Of The Polynomial Indicated Against Them I P X 3x Youtube




Ex 2 2 2 Find P 0 P 1 And P 2 For Each Of The Ex 2 2




Calameo Cambio De Variable 1º
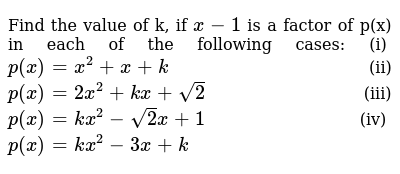



Find The Value Of K If X 1is A Factor Of P X In Each Of The Fo




Factoring 3x 4 2x 3 3x 2 Over The Complex Numbers Youtube




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes



Q Tbn And9gcsjb4sdrurp Fjggxxwvvnyqgndcwds5tn8cydbf5xaz91gznsw Usqp Cau




Problems 1 Consider The Random Variables X And Y Chegg Com




If Both X 2 And X Half Are Factors Px2 5x R Then Show That P R Brainly In



Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf




Inomat Verify Whether The Following Are Zeroes Of The Polynomial Indicated Against Them 1 P 3x 1 R It P A 1 1 1 1 I P X 5x 1 X 3 Iv P X X



What Will Be The Value Of P And Q For X 2 2x 5 To Be A Factor Of X 4 Px 2 Q Quora




Find The Zeros Of The Following Quadratic Polynomial P X 6x 2 X 6



Find The Value Of P For Which The Quadratic Equation 2p 1 X 2 7p 2 X 7p 3 0 Has Equal Roots Also Find These Roots Sarthaks Econnect Largest Online Education Community



2




Find Remainder Of Polynomial When Divided By X 2 3x 2 Remainder Theorem Application Youtube



For A Polynomial P X The Value Of P 3 Is 2 Which Of The Following Must Be True About P X The Answer Is D The Remainder When P X Is



The Polynomial P X X4 2x3 3x2 Ax 3a 7 When Divided By X 1 Leaves The Remainder 19 Studyrankersonline




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Polynomials Ppt Video Online Download



Studentportalen Uu Se Uusp Filearea Tool Download Action Nodeid Toolattachmentid 1960



0 件のコメント:
コメントを投稿